RESEARCH
Fundamentals and applications of statistical physics
Statistical physics bridges the gap between macroscopic and microscopic worlds, which originated in attempts to explain how the irreversible macroscopic behaviors can be reconciled with the reversible microscopic Hamiltonian equations of motion, in other words, why the entropy increases and how the direction of time arrow becomes certain. Statistical physics aims at a fundamental understanding of how the macroscopic collective properties emerge from interactions of many degrees of freedom, which cannot be simply deduced from an understanding of individuals. Representative examples of the emergent phenomena are phase transitions and criticalities, associated with singularities of thermodynamic functions, which signals the existence of universal physical mechanism underlying seemingly quite distinct systems. Contrary to other disciplines of physics, the scope of statistical physics is not restricted to specific systems but is rather unlimited and has found applications in broad areas, with considerable success, encompassing from solid-liquid-gas transitions of classical systems to macroscopic quantum effects such as superconductivity and superfluidity.
As stated above, we have witnessed the great triumphs of the equilibrium statistical physics in the 20th century. In this new era, the biggest challenges remained largely unexplored in the statistical physics are constructions of fundamental theories of nonequilibrium statistical mechanics and applications of statistical mechanics to realms beyond the traditional boundaries including social sciences and biological sciences. This defines the identity of us and what we explore: Based on statistical physics, we seek for theoretical understanding of fundamental principles underlying equilibrium or non-equilibrium behaviors of various systems, ranging from criticalities in the bio-soft matter to nonequilibrium quantum systems.
More specifically, subjects or research topics of our interests are largely categorized into:
Biophysics and soft matter
Biological systems are notorious for their complexities and have been considered at the outside the conventional boundaries of physics. They look very different from traditional physical systems such as ferromagnetic materials and carbon nanotubes, although basic constituents may have little difference on atomic scales. Life is emergent phenomena in the sense that biological systems consist of many constituents strongly interacting with each other and that their vivid life-giving functions cannot be understood as a simple sum of constituents. They indeed exhibit very different states, as results of interactions of many degrees of freedoms and small changes in ambient conditions, which is a prominent characteristic of phase transitions. We aim at answering whether diverse biological functions and processes can be described by very physical concepts of phase transitions and criticalities.
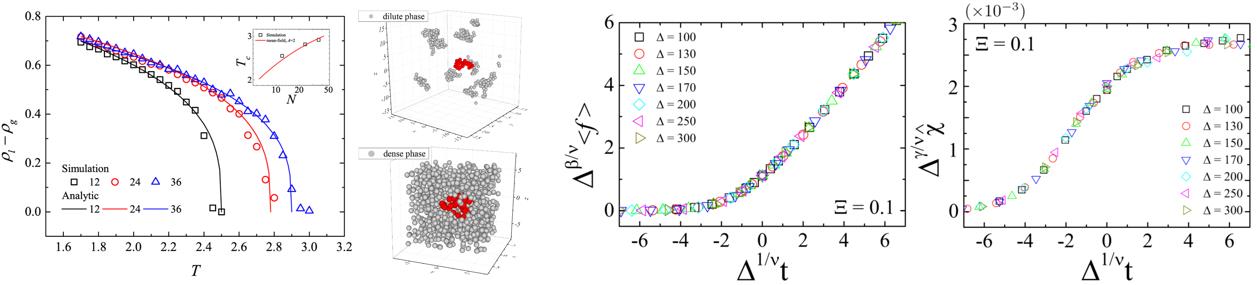
Hidden criticality of counterion condensation near a charged cylinder, Sci. Rep. (2017)
Scaling and criticality of the Manning transition, EPJE (2017)
Rodlike counterions at charged cylinders, Phys. Rev. Lett. (2018)
Materials with small elastic constants of the order of the thermal energy are called soft matter. Typical examples are polymers and membranes that constitute the one- and two-dimensional forms of life (proteins and cell membranes), respectively. Due to small bending elasticity, they are easily deformable and their equilibrium conformations are governed by competitions between energy and entropy. We are interested in statistical modeling of their conformations and of how they perform various biological functions using conformational flexibility.
Membrane curvature induced by polymer adsorption, Phys. Rev. E (2001)
Effects of charge fluctuation on two-membrane instability, Phys. Rev. Lett. (2003)
Fluctuations of red blood cell membranes, Phys. Rev. E (2015)
Transport through nuclear pore complex, Phys. Rev. E (2018)
Propulsion on the micro/nano-meter scale requires design principles very different from the macroscopic world. For example, the nonlinear inertia term in the Navier-Stokes equation is negligible on this scale, and one obtains the linear relationship between driving forces and resulting velocities. As a result, the nonlinear coupling of elasticity (of deformable soft objects) and hydrodynamic flow is a key factor to have a net thrust/propulsion by breaking time-reversal symmetry. Typical examples are flagella and cilia, widely used for motility of microorganisms and for fluid pumping by internal organs. Understanding the dynamics of micro-objects in hydrodynamic medium, far from equilibrium, is therefore essential in biology as well as in biotechnology (e.g., directed motion of nano-robots and mixing strategies in nano-chip-sized devices), to which physicist can make an important contribution. Despite its apparent importance, many aspects of low Reynolds number hydrodynamics on cellular biology in non-equilibrium situations are yet to be explored. This defines one direction of our research.
Electro-osmosis at inhomogeneous charged surfaces, J. Chem. Phys. (2006)
Nonlinear response of grafted semiflexible polymers in shear flow, Macromolecules (2009)
Chiral separation by flows: The role of flow symmetry and dimensionality, Sci. Rep. (2016)
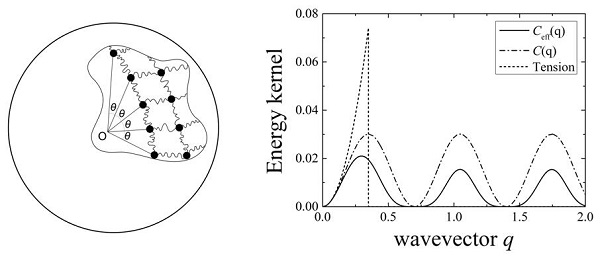
Electrostatic interaction is not only of great importance in industrial applications but also a prerequisite for biological functions. For instance, recent experimental evidences show that vesicles or liposomes of various types start to fuse, with multivalent ions like Ca2+ added above a threshold concentration of millimolar range. A similar phenomenon also occurs in vivo in the delivery of neurotransmitters at synapses of neurons. Electrostatic effects on biological systems and functions have thus been one of the most widely studied subjects in biological physics, but a number of important questions remain yet to be answered. Thus, electrostatic interactions in biological systems (Coulomb fluids in life) constitutes another direction of my future research. One of the goals is to reveal the role of electrostatic interaction (and correlation) in biologically-observed condensed phases and elastic properties of biopolymers. For instance, we want to understand Why rod-like polyamine ions are so effective in inducing the condensation of viruses and DNA (which can be viewed in a coarse-grained picture as charged cylindrical objects)?
Static and dynamic correlations in a charged membrane, Phys. Rev. E (2006)
Attractions between like-charged surfaces with dumbbell-shaped counterions, Phys. Rev. Lett. (2008)
Conformations of semiflexible charged chains, Phys. Rev. E (2010)
Rodlike counterions at charged cylinders, Phys. Rev. Lett. (2018)
Nonequilibrium statistical mechanics and stochastic processes
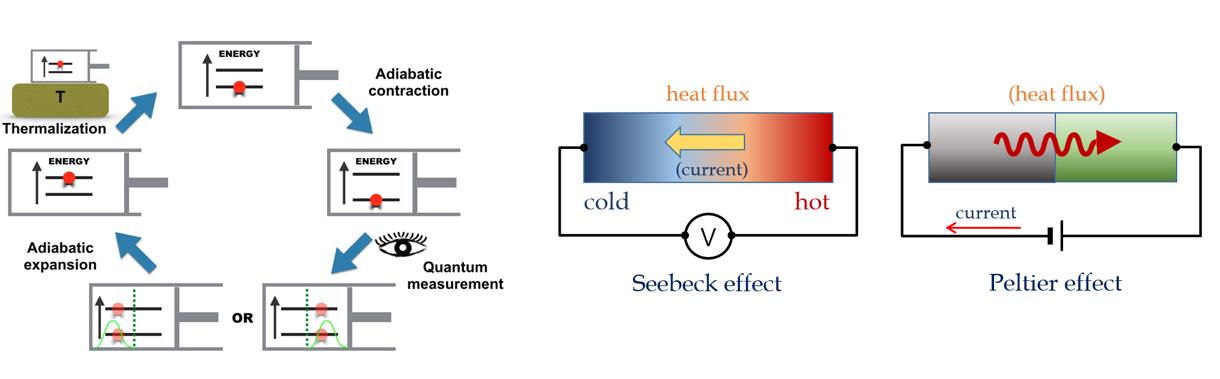
Comparison of free-energy estimators and dependence on dissipated work, Phys. Rev. E (2012)
Nonequilibrium work and entropy production by measurements, Phys. Rev. E (2013)
Initial ensemble dependence of Jarzynski equality in the thermodynamic limit, J. Phys. A (2015)
Single-temperature quantum engine without feedback control, Phys. Rev. E (2017)
Role of work in matter exchange between finite quantum systems, New J. Phys. (2017)
Role of measurement in feedback-controlled quantum engines, J. Phys. A (2017)
Measurement-driven single temperature engine, Phys. Rev. E (2018)
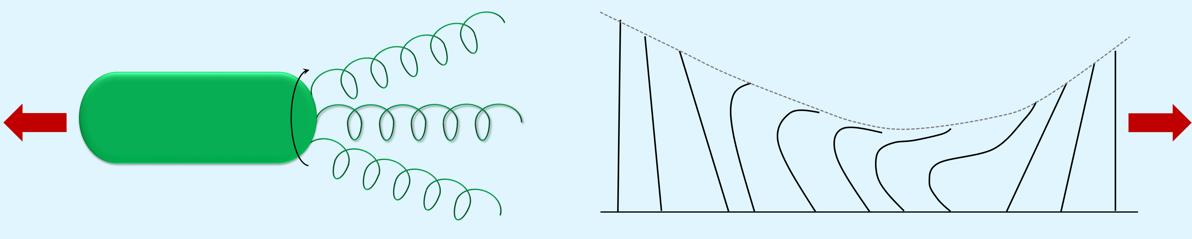
Pumping Fluids with Periodically Beating Grafted Elastic Filaments, Phys. Rev. Lett. (2006)
Hydrodynamic effects in driven soft matter, Soft Matter (2006)
In stochastic approach, the temporal evolution of a state is described by a probability theory where the fast degrees of freedom are integrated out and treated as random forces. The stochastic theory was originally formulated in attempts to describe the Brownian motions and the stock markets, and has provided a powerful tool for problems where the microscopic equation of motion is of no practical use or the Hamiltonian of a system cannot be properly defined. Let us consider a specific example: How long does it take for a random walker or a diffusing particle to first encounter a target? Although the statement of the problem appears simple, it is one of the representative problems in stochastic dynamics. In recent years, random target searching has received a great deal of attention in the context of the first-passage dynamics, and has been applied to abundant examples ranging from animal foraging, diffusion-limited chemical reactions to searching a missing child. Despite long-standing history, the general understanding of random target searching is still far from complete, and various aspects such as confinements, dependence of target location, mortality of searchers, mobility of targets, and parallel searching of multiple searchers are under active investigation.
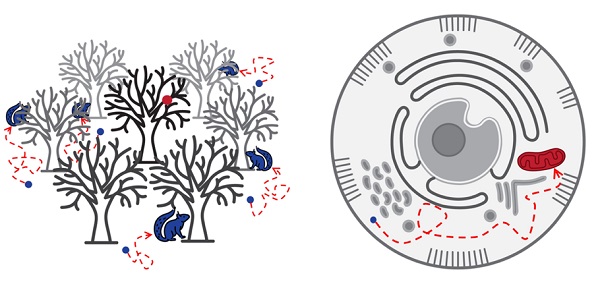
Parallel random target searches in a confined space, Phys. Rev. E (2017)
Public opinion by a poll process: model study and Bayesian view, J. Stat. Mech. (2018)
First-passage dynamics by aggregating particles, JKPS 79, 653 (2021)
Optimal searcher distribution for parallel random target searches, Phys. Rev. E 106, 024101 (2022)
Target searches of interacting Brownian particles in dilute systems, Phys. Rev. E 107, 064143 (2023)
Searching for a partially absorbing target by a run-and-tumble particle in a confined space, Phys. Rev. E 109, 014103 (2024)
Active search for a reactive target in thermal environments, J. Chem. Phys. 160, 044103 (2024)
Random search for a partially reactive target by multiple diffusive searchers, Phys. Rev. E 111, 014124 (2025)
Cellular medium constitutes a representative example of fluctuating, complex environments which host a variety of material and information transports. For instance, intercellular or intracellular protein transports occur in forms of transmembrane transports, vesicle transports, and nuclear transports. Considering these processes as diffusions over free energy barrier, we seek for fundamental understanding of underlying mechanisms from statistical physics point of view.
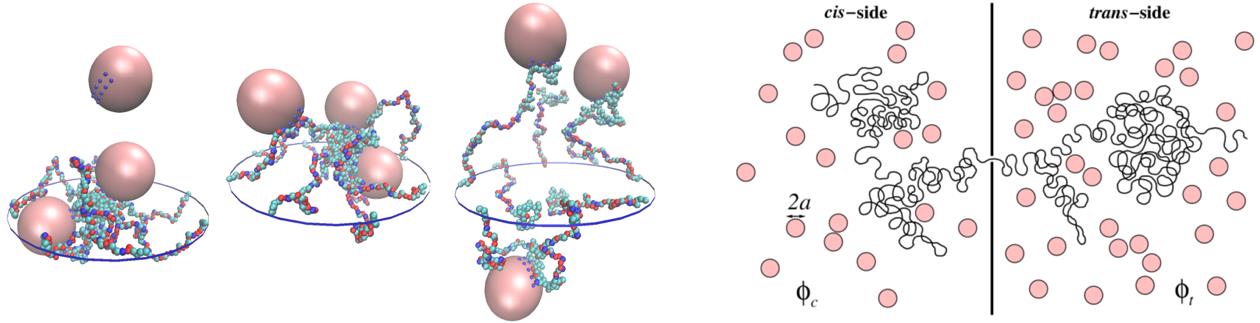
Polymer translocation in crowded environments, Phys. Rev. Lett. (2007)
Diffusion trajectories of anisotropic objects, J. Chem. Phys. (2015)
Selective and rapid transports through nuclear pore complex, Phys. Rev. E (2018)
Thermodynamics is the theory to understand and exploit the usage of heat-engine working in macroscopic world. In the quantum world, quantum fluctuations are important. Thermodynamic quantities such as heat, work, and entropy production are described by stochastic variables. We seek various study in discovering the thermodynamic laws that governs also for the microscopic quantum system, beyond the original scope of thermoynamics.
Entropies of the microcanonical ensemble, AIP advances 12, 065226 (2022)
Sum rule for fluctuations of work, Phys. Rev. E 110, 034108 (2024)
Observing quantum work by Margenau-Hill quasiprobability (accepted)







